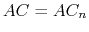Next: Examples Up: Declarative Loops and List Previous: Examples Contents Index
foreach(orin
,
,
in
,
,
,
)
foreach(wherein
,
,
in
,
,
,
)
One form of an accumulator is ac![]() , where
, where ![]() is a variable and
is a variable and ![]() is the initial value for the accumulator before the loop starts. In
is the initial value for the accumulator before the loop starts. In ![]() , recurrences can be used to specify how the value of the accumulator in the previous iteration, denoted as
, recurrences can be used to specify how the value of the accumulator in the previous iteration, denoted as ![]()
^0, is related to the value of the accumulator in the current iteration, denoted as ![]()
^1. Let's use
![]() to denote an instance of
to denote an instance of ![]() in which
in which ![]()
^0 is replaced with a new variable ![]() ,
, ![]()
^1 is replaced with another new variable ![]() , and all local variables are renamed. Assume that the loop stops after
, and all local variables are renamed. Assume that the loop stops after ![]() iterations. Then this foreach means the following sequence of goals:
iterations. Then this foreach means the following sequence of goals:
=
,
,
,
,
,