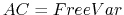Examples

   ?-foreach(I in [1,2,3],ac(S,0),S^1 is S^0+I).
   S = 6

   ?-foreach(I in [1,2,3],ac(R,[]),R^1=[I|R^0]).
   R = [3,2,1]

   ?-foreach(A in [a,b], I in 1..2, ac(L,[]), L^1=[(A,I)|L^0]).
   L = [(b,2),(b,1),(a,2),(a,1)]

   ?-foreach((A,I) in ([a,b],1..2), ac(L,[]), L^1=[(A,I)|L^0]).
   L = [(b,2),(a,1)]

The following predicate takes a two-dimensional array, and returns its minimum and maximum elements:

    array_min_max(A,Min,Max):-
        A11 is A[1,1],
        foreach(I in 1..A^length, 
                J in 1..A[1]^length, 
                [ac(Min,A11),ac(Max,A11)],
                ((A[I,J]<Min^0->Min^1 is A[I,J];Min^1=Min^0),
                 (A[I,J]>Max^0->Max^1 is A[I,J];Max^1=Max^0))).

A two-dimensional array is represented as an array of one-dimensional arrays. The notation A^length means the size of the first dimension.

Another form of an accumulator is $ac1(AC,Fin)$, where $Fin$ is the value $AC_n$ takes on after the last iteration. A foreach call with this form of accumulator means the following sequence of goals:

		 		 $AC_0$ = $FreeVar$, 

$Goal(AC_0,AC_1)$, 

$Goal(AC_1,AC_2)$, 

$\ldots$, 

$Goal(AC_{n-1},AC_n)$, 

$AC_n=Fin$, 

$AC=FreeVar$

We begin with a free variable $FreeVar$ for the accumulator. After the iteration steps, $AC_n$ takes on the value $Fin$ and the accumulator variable $AC$ is bound to $FreeVar$. This form of an accumulator is useful for incrementally constructing a list by instantiating the variable tail of the list.